Why Does Total Internal Reflection Happen?
Most recent answer: 01/30/2016
- Aaryan Dewan (age 16)
Jalandhar, INDIA
I've been thinking about this all day! You're right, the "sine function can't be greater than 1" argument is pretty unsatisfying as a physical explanation. Here's something a little more physical, although it still isn't the whole story.
As you know, when light traveling through a material hits a boundary with another material that has a lower index of refraction—a boundary between water and air, for example—the light refracts (bends). The refraction angle depends on the angle between the incident light and the boundary. At the critical angle, the light bends so much that it emerges parallel to the boundary between the two materials.
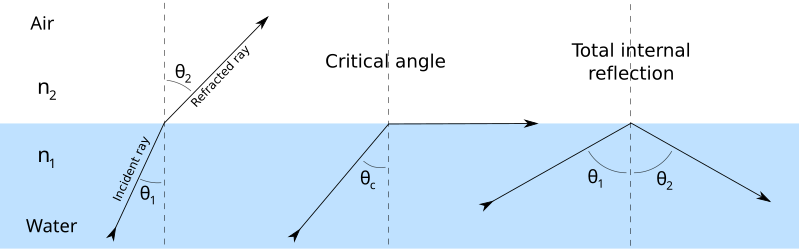
At any angle larger than the critical angle, the bending of the light would bring it back into the first material. That's the key physical observation. It's not just that the sine function in Snell's law can't be greater than one, but also that any further bending of the light would bring the refracted beam back into the first material. Water has a different index of refraction than air does, so the behavior of the light is different as soon as it goes back into the water. That's why the angle of refraction suddenly "jumps" from 90 degrees to an angle equal to the incident angle.
To understand why light does this bending and reflecting at all, we can solve Maxwell's equations at the boundary of two materials with different indices of refraction. That's where the electrons come in—the way they oscillate in an electromagnetic field in different materials determines the index of refraction, and how light will behave at a boundary. The more complete story is that even at angles smaller than the critical angle, some light is reflected back into the first material, and the reflection and transmission depend on the polarization of the light. At angles greater than the critical angle, some of the electric field still makes it through the boundary, but it dies off exponentially with distance. This chapter of the Feynman lectures has a nice discussion of reflection and transmission from surfaces: http://www.feynmanlectures.caltech.edu/II_33.html
Rebecca H.
(published on 01/30/2016)