Centrifugal Forces on a String
Most recent answer: 06/10/2011
Q:
About centripetal force, or the tension on a string with a stone tied at the far end, and being swung around in a circle.
The centripetal force needed to balance the centrifugal force of the stone is mv^2/r, and the inward acceleration is v^2/r.
Does this apply whatever other forces are at work, in a universal way? Or would, say, air resistance make the inward acceleration v^2/r different? Or for instance, if the stone were being swung around underwater, how would this affect the formula v^2/r? Would one simply use the slower speed for v, and find that the formula still worked?
Thank you very much, best wishes, David Martin
- David Martin (age 37)
AZ
- David Martin (age 37)
AZ
A:
Hello David,
The instantaneous force on the string is, as you say, mv2/r. Air and water resistance have the effect of slowing the mass down and affect the time derivative of the force. Air resistance force is perpendicular to the string and therefore does not affect the tension at that moment.
If you know the velocity dependence of the force of air or water on the moving mass then you can write a differential equation for the time dependence of the velocity: dv/dt = -F(v)/m and get an idea how the force on the string depends on time.
LeeH
The instantaneous force on the string is, as you say, mv2/r. Air and water resistance have the effect of slowing the mass down and affect the time derivative of the force. Air resistance force is perpendicular to the string and therefore does not affect the tension at that moment.
If you know the velocity dependence of the force of air or water on the moving mass then you can write a differential equation for the time dependence of the velocity: dv/dt = -F(v)/m and get an idea how the force on the string depends on time.
LeeH
(published on 06/10/2011)
Follow-Up #1: More on centrifugal forces and acceleration
Q:
Thankyou. I understand that the time derivative would be different, but the question was simply about the instantaneous force on the string. To calculate that, if a stone is being swung around at a constant speed on a string underwater, would one use mv^2/r, but simply put in the slower speed for v? In other words, is that aspect of things exactly the same as if one were just swinging the stone around more slowly, but through air?
It seems that this is the case from your answer, which makes good sense. The reason I thought it might be otherwise is that v^2/r is a radial acceleration, and although nothing actually moves radially, if there were any radial motion it too would be affected by the drag force of the water. So I wondered if that meant an adjustment would be needed. But perhaps there is a cancellation, leaving mv^2/r the same. Or perhaps mv^2/r is the same, but just anyway. Please clarify this if possible, thank you very much.
- David Martin (age 37)
AZ
- David Martin (age 37)
AZ
A:
Hello again David,
You are correct in observing the radial length is not changing, however, the acceleration is a vector, the time derivative of another vector, velocity. For a particle moving at constant speed in a circle the magnitude of the velocity does not change, but the direction does. This constitutes acceleration. The direction of this acceleration is in the radial direction.
Here is a diagram that I swiped from :
Notice that the little green vector labeled Δv is in the radial direction.I hope this helps.
LeeH
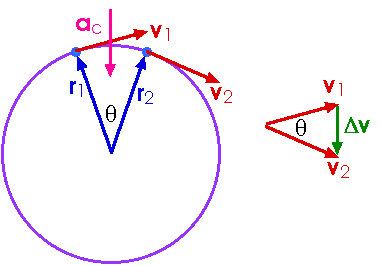
You are correct in observing the radial length is not changing, however, the acceleration is a vector, the time derivative of another vector, velocity. For a particle moving at constant speed in a circle the magnitude of the velocity does not change, but the direction does. This constitutes acceleration. The direction of this acceleration is in the radial direction.
Here is a diagram that I swiped from :
Notice that the little green vector labeled Δv is in the radial direction.I hope this helps.
LeeH

(published on 06/16/2011)