Why Does the Moon Orbit the Earth and not the Sun?
Most recent answer: 12/21/2011
- farnoosh (age 17)
Karaj, Alborz, IRAN
Hi Farnoosh,
That's a great question! You're correct that the Sun exerts roughly twice as much gravitational force on the Moon as does the Earth. You can calculate that from Newton's Law of Universal Gravitation by comparing M/R2 to m/r2, where R is the distance from the Sun, r is the distance from the Earth to the Moon, M is the Sun's mass, and m is the Earth's mass. As it turns out, however, that force comparison is meaningless in this context.
Imagine the Earth-Moon system exists in a completely uniform gravitational field. The motion of the Moon around the Earth would continue as it does now, with the field doing nothing to change their relative positions. In fact, the Moon would orbit the Earth in precisely the same way that it would if there were no background uniform gravitational field at all. It follows that what matters is not the average field that the sun exerts on the Earth-Moon system, but how much that field changes from place to place. It's these changes that cause the bodies to accelerate differently, and thus affect how the Moon moves relative to the Earth.
Since the force from the Sun falls off as 1/R2, its spatial derivative does so as 1/R3. The difference between the field at the Earth and the Moon is then roughly r/R times the field at the Earth, where r is the size of the Moon's orbit. Thus the question becomes whether or not that difference is as large as the field from the Earth. If it is, then the different Sun-caused accelerations of the Moon and Earth are substantial enough to make a big difference in their orbits. So, roughly speaking, the question is whether M/m is about as big as (R/r)3, where M is the Sun's mass and m is the Earth's mass. The answer, as it turns out, is no. As you noted, M/m is a bit bigger than (R/r)2.
So the Moon orbits the Earth almost the same way it would if they were isolated. Meanwhile, both the Earth and the Moon orbit the Sun together.
Applying this concept in detail, we find the following:
When three bodies interact gravitationally, their motion is determined by position relative to what is known as the Hill Sphere of each. A body's Hill Sphere is the region in which the gravitational influence of that body is more important than the influence of other (often larger) bodies nearby. It is determined by the masses of the different bodies, and the semi-major axis (or "major radius", the radius as measured along the longest part of an ellipse, as seen below) and eccentricity of orbit (i.e. how far the orbit is from perfectly circular).
(image source: )
If we assume a roughly circular orbit, the radius of the Hill Sphere is given by
rH = a*(m/3M)^(1/3), where m is the mass of the smaller body (in this case, the Earth), M is the mass of the larger body (the Sun) and a is the semi-major axis.(Note that this is just what our rough argument above gave, but now with the numerical factor (1/3)^1/3 included.)
Wikipedia offers a nice visualization, seen below, though it's worth noting that it's not to scale. The points labeled L1-L5 show where a body would potentially leave orbit if its radius exceeded that of the Hill Sphere.
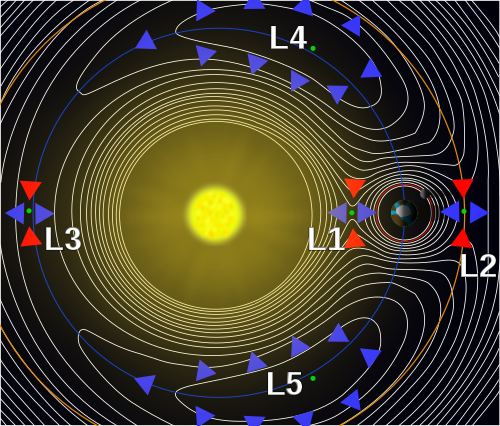
But that's enough talk for now... Here's a simulator that approximates a roughly circular orbit: Plug the masses of the Sun and Earth in and play around with the distance a bit!
I hope that answers your question!
Best,
Becca
(published on 12/21/2011)