Quantum Degeneracy
Most recent answer: 07/13/2015
- Nitin (age 17)
Hoshiarpur, Punjab,India
Here "degeneracy" just means that more than one state share the same energy level. The number given for the degeneracy should just be the number of states with the same energy.
I do not think the number "9" is correct in any approximation, however. The energies of the excited states of helium are described here: http://hyperphysics.phy-astr.gsu.edu/hbase/quantum/helium.html. Here's a figure borrowed from that site.
Helium Energy Levels
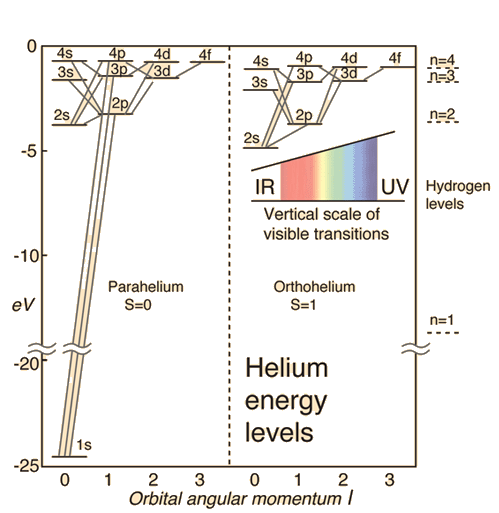
The electron energy levels for a helium atom demonstrate a number of features of multi-electron atoms.
One electron is presumed to be in the ground state, the 1s state. An electron in an upper state can have spin antiparallel to the ground state electron (S=0, singlet state, parahelium) or parallel to the ground state electron (S=1, triplet state, orthohelium).
Notice that the second state up from the bottom is the 2S S=0 parahehelium state. So technically that's the second energy level from the bottom. There's only one such state, the degeneracy is 1. Now probably what the people you heard are doing is grouping the states into almost degenerate batches: the "1" state, the "2" states, the "3" states,... So probably what they're saying is that there's 1 3s state, three 3p stats, and 5 3d states, with the different numbers giving how may distinct ways the orbital angular momentum can be arranged.
There are two problems with their claim. First, as you can see in the illustration, the energies are not the same, so the states aren't degenerate. Second, their choice to ignore the spin is peculiar. Nature doesn't ignore the spin. For example, if we consider the 3s para and 3d ortho energies very nearly equal, in thermal equilibrium there will be 15 times as many atoms in the 3d ortho states as in the 3s para state, because not only does the latter have 5 orbital versions, it also has 3 spin versions.
Mike W.
(published on 07/13/2015)